Il progetto si pone l'obbiettivo di analizzare un algoritmo di backtracking.
Parte dell'analisi consiste nella visualizzazione delle soluzioni parziali del problema e
come esse evolvano durante l'esplorazione dello spazio delle soluzioni con l'aiuto di un albero.
Il problema considerato è quello del labirinto.
Consideriamo una matrice binaria NxM dove siano assegnate due posizioni particolari (entrata ed uscita dal labirinto).
Le celle della matrice possono essere dei vicoli cechi o delle celle percorribili.
Scopo del problema è quello di individuare un percorso composto da celle percorribili adiacenti che colleghi entrata ed uscita dal labirinto.
Il problema in esame si presta ad una soluzione ricorsiva.
L'idea è di costruire una funzione ricorsiva che esplori il labirinto incrementalmente e controlli
che l'uscita del labirinto sia stata raggiunta. Se il percorso porta invece ad un vicolo cieco,
questa soluzione viene scartata e un nuovo percorso è esplorato a partire dall'ultima posizione ancora aperta.
L'algoritmo per creare e risolvere un labirinto è liberamente ispirato da Coding challenge #10 (2 weeks): Maze generation
(https://www.reddit.com/r/prolog/comments/g4tdav/coding_challenge_10_2_weeks_maze_generation/)
[Video]
Il cuore del programma è costituito dal solver, cioè una funzione che prende in ingresso un labirinto
propriamente inizializzato e restituisce una soluzione,
assieme a tutte le informazioni necessarie per la visualizzazione.
Camminando all'interno del labirinto è possibile procedere in quattro direzioni:
- sinistra
- destra
- alto
- basso
purchè la cella di arrivo sia percorribile. Nessun vincolo ulteriore è stabilito.
Il programma si divide in 3 parti:
- creazione del labirinto
- lancio del solver
- visualizzazione della soluzione
CREAZIONE DEL LABIRINTO
Un nuovo labirinto è creato con la funzione drow_maze(n, m, Y)

La funzione accetta come argomenti la dimensione del labirinto e salva in Y la matrice del labirinto.
Nella presente implementazione, il labirinto è rappresentato da due liste annidate:
Colonna(
Riga(#,#," ", #),
Riga(#,#," ", #),
Riga(#,#," ", #),
...
Riga(#,#," ", #),
)
- la lista esterna di lunghezza n rappresenta le n colonne della matrice
- la lista corrispondente a una colonna, diciamo i, rappresenta la riga i di dimensione m.
Gli elementi delle celle nella lista annidata (le righe) possono essere:
- il carattere spazio " " (cella percorribili)
- il carattere "#" (muro)
Per comodità si suppone che esista un unico ingresso del labirinto nella prima riga
ed un'unica uscita localizzata nell'ultima riga.
La costruzione del labirinto è perciò soggetta a due vincoli ulteriori:
- Il perimetro del labirinto è costituito da celle piene
- la prima e l'ultima riga hanno ciascuna esattamente una cella vuota. Queste celle sono scelte casualmente con la funzione random_between
LANCIO DEL SOLVER
Passaggio 1 - INIZIALIZZAZIONE SOLVER
Prima di poter far partire la ricorsione, è necessario inizializzare la posizione della partenza e dell'arrivo.
Il predicato find_start_end_point(Maze, Start, End) serve ad inizializzare le due variabili
Start ed End necessarie al solver.
La funzione cerca le caselle vuote nella prima e nell'ultima riga.
L'implementazione in PROLOG è composta da 5 possaggi in AND:

PASSO PASSO > find_start_end_point
Per prima cosa vengono salvate il numero di righe della matrice nella variabile Y2 con l'ausilio del predicato functor(x,y,z).
Il predicato functor(x,y,z) conta gli argomenti (arity) della funzione X e li salva nella variabile z.
Nel nostro caso, la variabile Maze è una struttura così composta:
c(
r(1,2,3,4),
r(1,2,3,4),
r(1,...)
....
r(1,2,3,4)
)
Quindi gli argomenti della funzione c() sono esattamente le colonne del labirinto.
Successivamente viene trovato l'indice dello spazio nella prima riga.
Questo passaggio si compone di due fasi in cui il predicato arg viene usato in 2 modi differenti:
- Salva la prima riga nella variabile FirstRow
In questo caso arg(i, x, y) estrae da una struttura X l'argomento con indice i.
Facendo riferimento alla sintassi di un linguaggio derivante dal C la scrittura arg(i, x, y) equivale a
FirstRow = X[i]
- Successivamente arg(X1,FirstRow, ' ') salva nella variabile X1 l'indice del primo spazio
(ovvero il valore da cercare) che viene trovato nella lista FirstRow.
Similmente si trova l'indice dello spazio nell'ultima riga.
Codice Prolog
arg(X1,FirstRow, ' ') -> setta nella variabile X1 l'indice del primo spazio (ovvero il valore da cercare) che viene trovato nella lista FirstRow.

arg(Y2,Maze, LastRow) -> setta nella variabile LastRow l'ultima riga.
arg(X2, LastRow, ' ') -> setta nella variabile X2 l'indice del primo spazio (ovvero il valore da cercare) che viene trovato nella lista LastRow
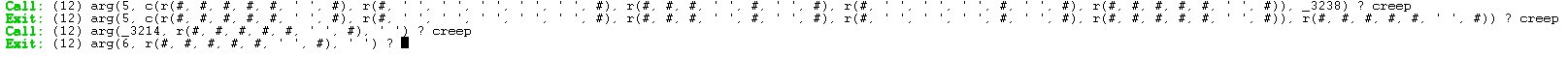
I valori di Start End sono salvati come coppia di punti separati dal carattere -
- Start: X1-1 > indice dello spazio - riga 1
- End: X2-Y2 > indice dello spazio - ultima riga
Passaggio 2 - ANALYSIS DEL SOLVER
Successivamente viene chiamata la funzione solve_maze_naive. Questa è la funzione che si occupa effettivamente di trovare l'uscita

Passaggio 2A
La prima istruzione serve a controllare che non si sia raggiunta l'uscita con: \+ CurrentPos == EndPos
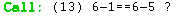
Se il confronto fallisce, si cerca di effettuare un passo nel labirinto.
Passaggio 2B
Viene eseguito mark_pos(Maze, CurrentPos, 'x'),. Questa funzione segna con il simbolo 'x' la posizione passata come argomento

PASSO PASSO > mark_pos(Maze, CurrentPos, 'x')
arg recupera la lista riga dalla variabile Maze.
nb_setarg() scrive nella lista la posizione corrente.
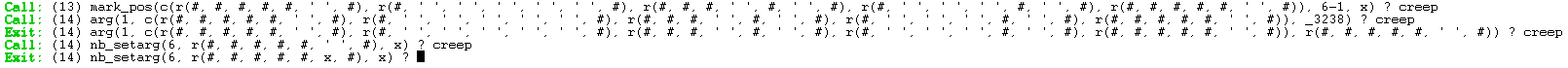
Quando la procedura termina la variabile Maze è stata modificata, con l'aggiunta della x nella posizione corrente.
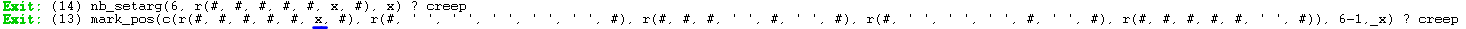
Passaggio 2C
Successivamente viene stampata a video la nuova matrice, con la funzione drawScreen(Maze),
Passaggio 2D
La successiva funzione è find_next_space(Maze, CurrentPos, NextPos), [3 argomenti]
Questa funzione prova a spostarsi a destra > sinistra > su > giù controllando che la casella sia vuota.

Le varie procedure find_next_space sono tra loro in OR, quindi finchè una di esse non restituisce true
vengono provate tutte.
La prima procedura che viene chiamata è quella che controlla la casella alla sua destra.
Ogni procedura find_next_space
come prima operazione calcola la casella successiva con la chiamata al predicato succ.
- Se voglio andare a destra succ sarà fatto sulla coordinata delle X e il valore incrementato di 1
- Se voglio andare a sinistra succ sarà fatto sulla coordinata delle X e il valore decrementato di 1
- Se voglio andare su succ sarà fatto sulla coordinata delle Y e il valore incrementato di 1
- Se voglio andare giù succ sarà fatto sulla coordinata delle Y e il valore decrementato di 1
Proviamo a seguire passo passo il comportamento della funzione find_next_space con questa nuova matrice. La coordinata di ingresso è 4-1
PASSO PASSO > find_next_space(Maze, CurrentPos, NextPos)
In questa immagine si possono vedere tutte le operazioni
che prolog esegue quando viene chiamata la funzione find_next_space() per la prima volta
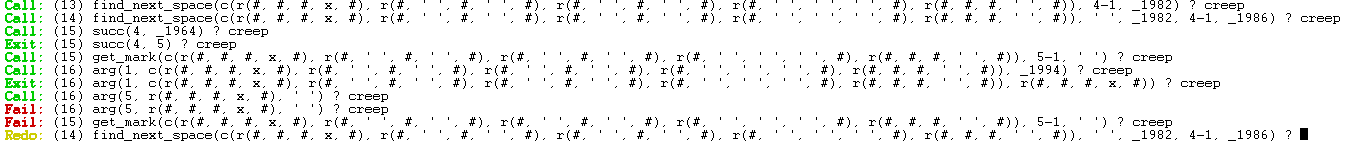
In posizione (13) viene chiamata la procedura find_next_space(3) [quella che ha solamente 3 argomenti].
(14) Questa procedura chiama nuovamente la procedura
find_next_space(5) [questa volta la procedura con 5 argomenti]
In questo passaggio la variabile Kind è stata settata a ' ': il valore assegnato ad una casella vuota.
Una volta ottenuta la coordinata della mossa successiva viene chiamata la funzione get_mark
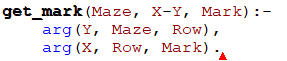
Questa funzione confronta se la casella di destinazione è uguale a ' ' (il simbolo di casella vuota)
Se il confronto fallisce bisogna
chiamare nuovamente la funzione find_next_space, questa volta però
cercando in un'altra direzione.
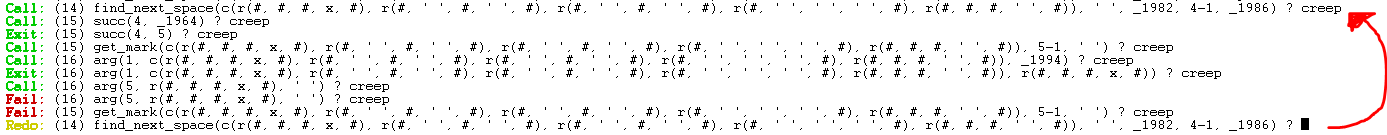
Nell'immagine precendente la procedura che è fallita sullo stack è la numero 16.
Fallendo la n° 16, prolog prova a concludere la procedura chiamante (n° 15) ma anche questa fallisce.
Ora sullo stack c'è la procedura n°14 [find_next_space()]
Ci sono 4 procedure chiamate find_next_space in OR.
Prolog chiama la procedura "find_next_space" successiva.
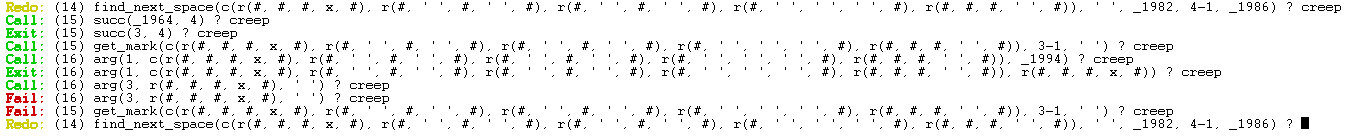
Anche in questo caso find_next_space fallisce perchè cerca di andare a destra e trova un muro.
Viene chiamata nuovamente la procedura find_next_space
La successiva procedura cerca di andare in basso nel labirinto e questa volta ha successo.

Passaggio 2E
Continuando nell'esecuzione del programma, visto che è stato effettuato un passo,
la funzione solve_maze_naive() richiama ricorsivamente se stessa ricominciando tutti i passaggi.
[sono nella cassella 'esci' (NO) -> segna dove sono -> fai un passo avanti -> sono nella cassella 'esci' (NO) -> segna dove sono -> fai un passo in avanti .... ]

Backtracking (da Trace)
PASSO PASSO
Nella seguente mappa è stato segnato il percorso che ha già fatto l'argoritmo.
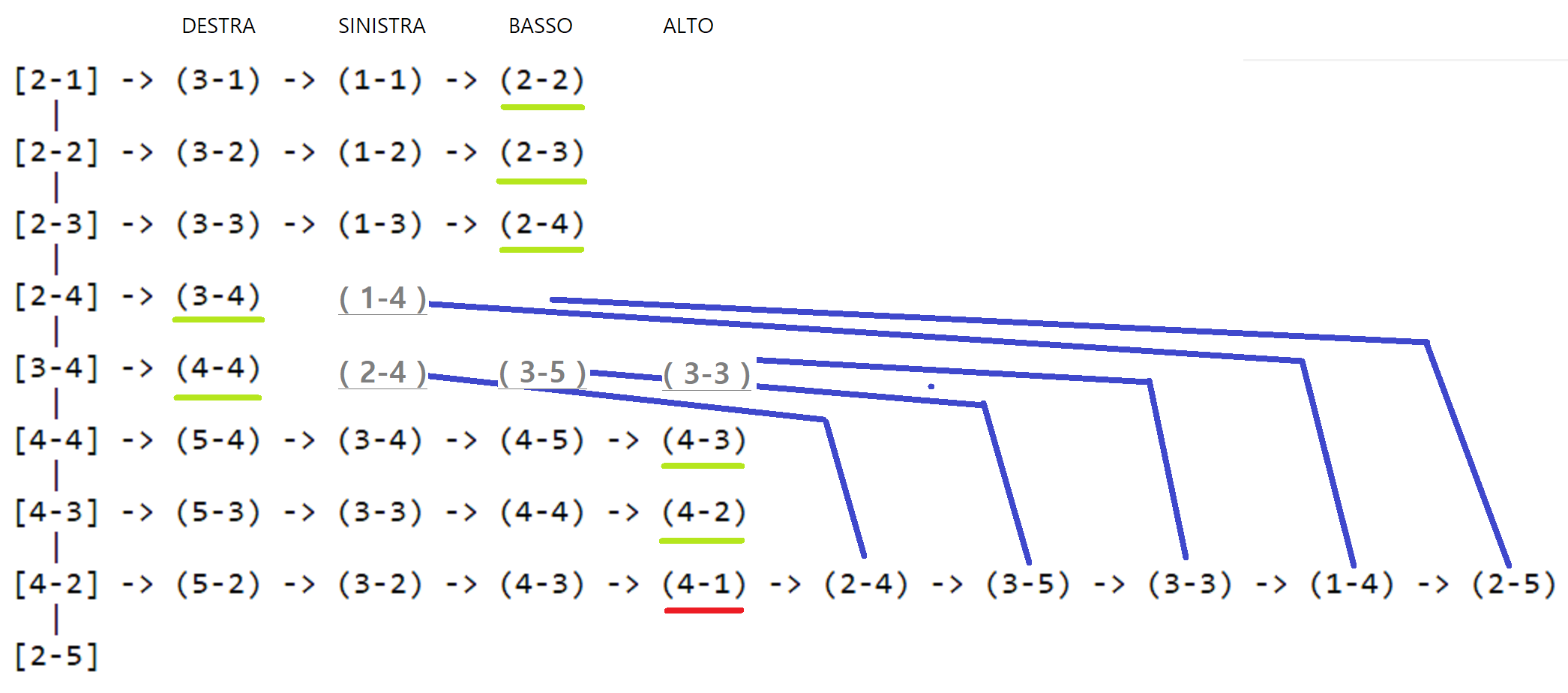
In questo altro screenshot si può vedere come funziona il backtracking:
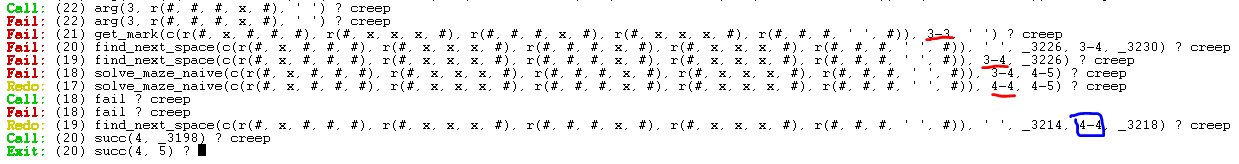
L'algoritmo nella casella 4-4 prende il corridoio di destra,
quando però arriva alla fine del corridio (2-4) non può piu avanzare in nessuna direzione.
Nell'immagine si vede che l'argoritmo prova con l'ultima casella
(3-3) delle 4 che deve testare.
Fallita la procedura il programma rimuove dallo stack la posizione (2-4) e
prosegue con la procedura successiva che trova sullo stack.
Però anche il passo successivo presente sullo stack (3-4) fallisce.
Il programma procede togliendo dallo stack quest'altro
punto e prova con il successivo.
Arrivato al nodo (4-4) l'algoritmo testa la casella in basso e finalmente raggiunge l'uscita.
VISUALIZZAZIONE DELLA SOLUZIONE
Un altro 'goal' del programma è far visualizzare tutte le decisioni che prolog ha preso.
Per questo è stato leggermente modificato l'algoritmo per poter visualizzare tutte le scelte fatte.
Il risultato è:
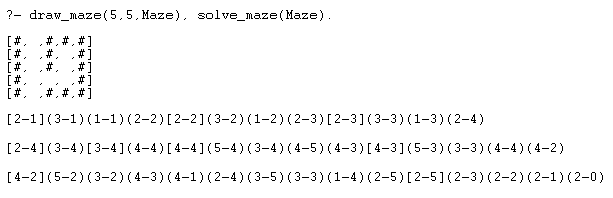
La prima coppia di valori rappresenta l'entrata, l'ultima coppia rappresenta l'uscita
Ogni coppia è racchiusa da parentesi. Se le parentesi sono quadrate allora il punto è stato preso,
la parentesi tonda invece vuol dire che la coppia è stata testata.
[2-1](3-1)(1-1)(2-2)[2-2](3-2)(1-2)(2-3)[2-3](3-3)(1-3)(2-4)[2-4](3-4)[3-4](4-4)[4-4](5-4)(3-4)(4-5)(4-3)[4-3](5-3)(3-3)(4-4)(4-2)[4-2](5-2)(3-2)(4-3)(4-1)(2-4)(3-5)(3-3)(1-4)(2-5)[2-5](2-3)(2-2)(2-1)(2-0)
Se volessimo rapprentare la visita nel labirinto con il programma notepad, il risultato sarebbe:
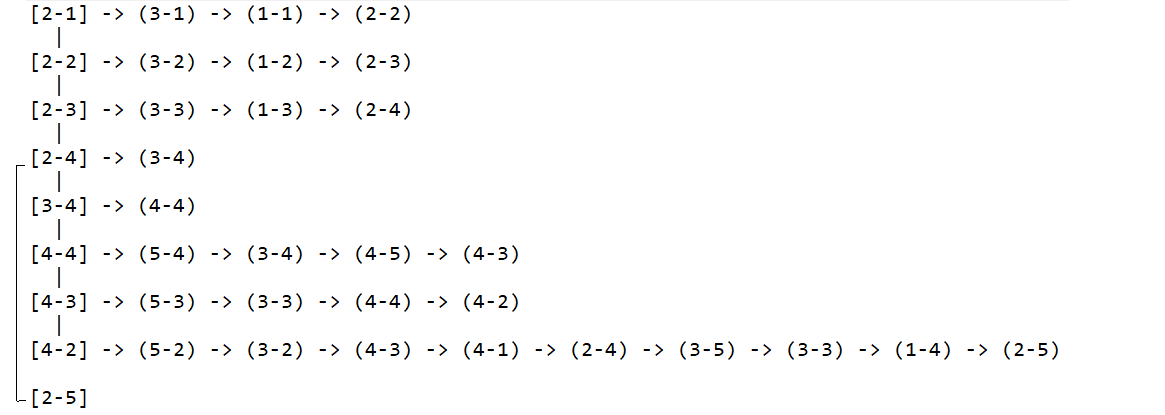
Nella seguente immagine si vede il backtracking
Finchè ci sono caselle libere il programma prosegue nella ricerca dell'uscita.
Il problema nasce quando deve controllare se la casella 4-1 è libera.
Sono finiti i passi disponibili tra destra, sinistra alto ed basso.
Tutta la procedura fallisce e quindi si prova a vedere nel passo precedente.
Anche in questo caso però tutti i passi erano stati già testati
quindi si prova di nuovo con la procedura precedente.
Arrivato al punto 3-4 l'algorirmo testa gli altri punti che erano rimasti da provare.
Non avendo trovato nemmeno una casella libera, la procedura fallisce.
Ora i passi che partono dal punto 2-4 vengono testati.
Questa volta il passo successivo è l'uscita e quindi l'algoritmo ha trovato la soluzione.
Visualizzare l'albero in prolog
Prolog permette di visualizzare i grafi grazie ad una funzione
(quasi) nativa "The GraphViz renderer"
[ https://swish.swi-prolog.org/example/render_graphviz.swinb]
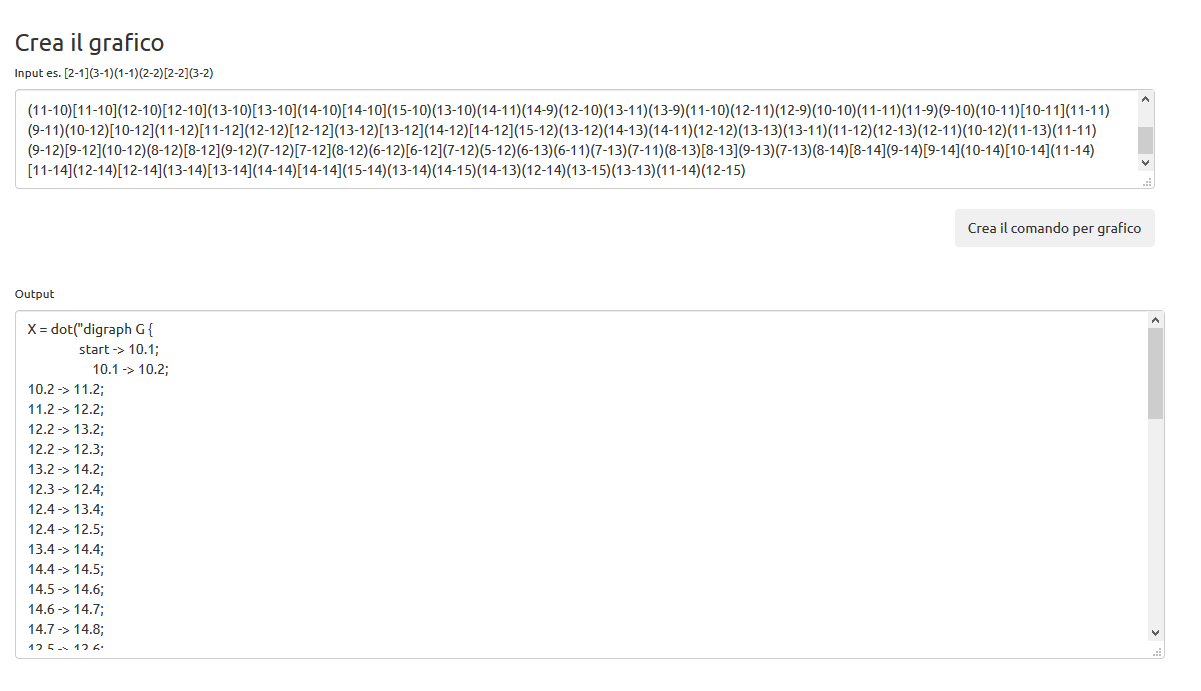
Si è creato un piccolo script per generare il comando che ne permetta
la visualizzazione.
Lo script prende in ingresso la lista dei punti testati dall'algoritmo:
[2-1](3-1)(1-1)(2-2)[2-2](3-2).... e restituisce il comando in prolog.
L'albero che mostra le scelte prese nel precendete labirinto è:
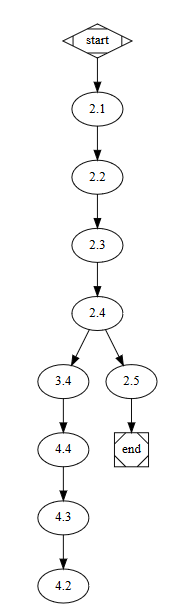
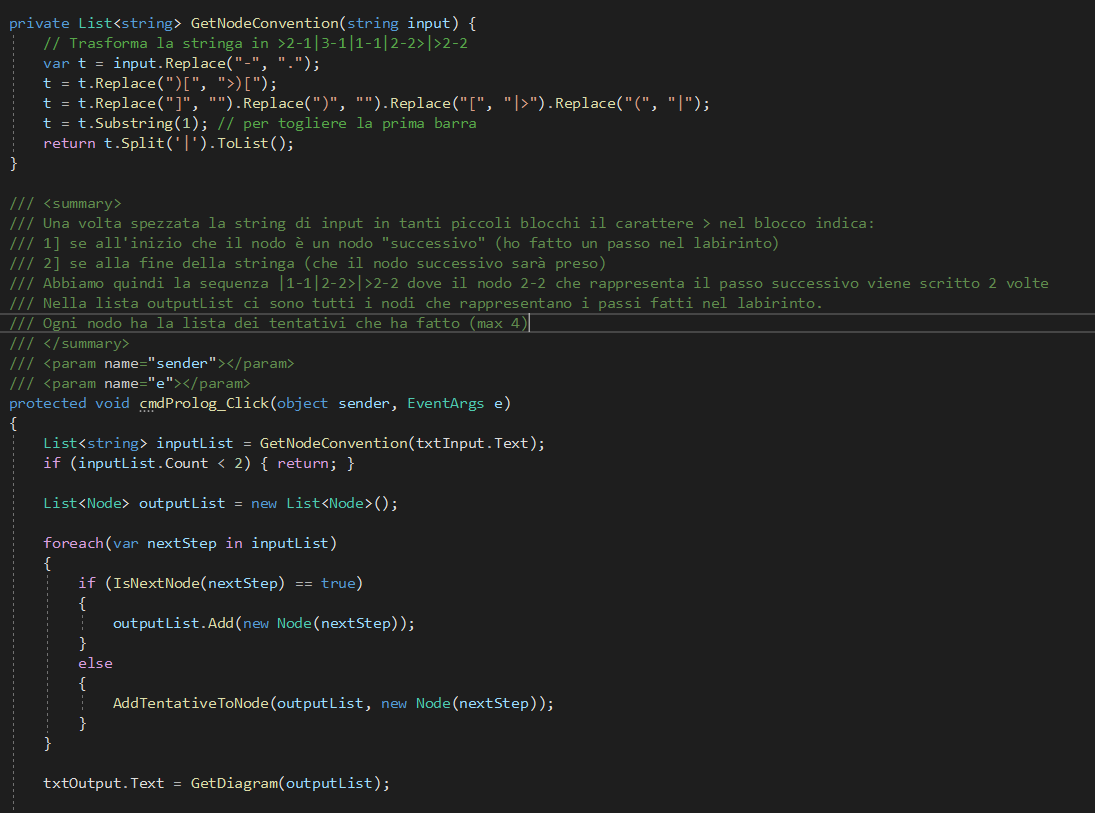
Il codice prolog che lo ha creato è:

Il codice per la creazione del comando per generare il grafo,
è stato sviluppato in C#. Nel riquadro 'Crea il grafico' in fondo alla pagina
è disponibile una versione online.
Esempio completo
In questo paragrafo c'è un esempio completo con un labirinto di dimensioni maggiori (15x15).
1) Viene creato e risolto il labirinto [Video]
2) Come output visivo, oltre al labirinto, c'è anche la variabile Maze

3) La variabile Maze è passata alla funzione show_maze, che visualizza tutti i tentativi ed i passi fatti dall'algoritmo.
Prima di essere passata al predicato show_maze, viene cancellata la strada percorsa nel labirinto
(le x vengono sostituite con il carattere ' ' )

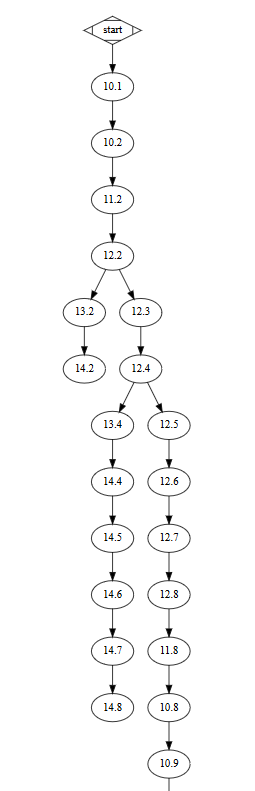
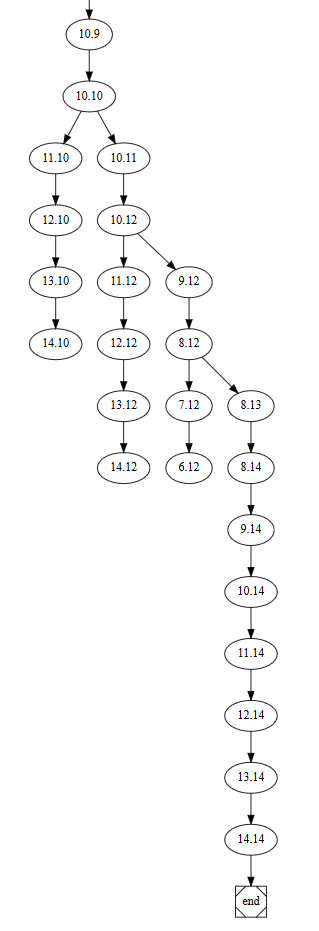
4) I passi fatti nel labirinto scritti nella forma [2-1](3-1)(1-1)(2-2)[2-2](3-2) vengono dati come input allo script per generare l'albero.
5) Il comando di prolog viene eseguito e produce l'albero che è stato percorso per trovare l'uscita
La variabile Maze di questo esempio:
Maze = c(r(#, #, #, #, #, #, #, #, #, x, #, #, #, #, #), r(#, ' ', ' ', ' ', #, ' ', ' ', ' ', ' ', x, x, x, x, x, #), r(#, ' ', #, #, #, #, #, #, #, #, #, x, #, #, #), r(#, ' ', ' ', ' ', #, ' ', ' ', ' ', #, ' ', #, x, x, x, #), r(#, ' ', #, ' ', #, ' ', #, ' ', #, ' ', #, x, #, x, #), r(#, ' ', #, ' ', #, ' ', #, ' ', ' ', ' ', #, x, #, x, #), r(#, ' ', #, ' ', #, ' ', #, ' ', #, ' ', #, x, #, x, #), r(#, ' ', #, ' ', #, ' ', #, ' ', #, x, x, x, #, x, #), r(#, ' ', #, ' ', #, ' ', #, ' ', #, x, #, #, #, #, #), r(#, ' ', #, ' ', ' ', ' ', #, ' ', #, x, x, x, x, x, #), r(#, #, #, #, #, #, #, #, #, x, #, #, #, #, #), r(#, ' ', #, ' ', #, x, x, x, x, x, x, x, x, x, #), r(#, ' ', #, ' ', #, #, #, x, #, #, #, #, #, #, #), r(#, ' ', ' ', ' ', ' ', ' ', ' ', x, x, x, x, x, x, x, #), r(#, #, #, #, #, #, #, #, #, #, #, o, #, #, #)).