ENGLISH FOR COMPUTER SCIENCE

Fidelity vs. Simplicity : a Global Approach to Line Drawing Vectorization

1 Introduction

Vector advantages: precision, compact and resolution-independent, easy to edit, the input of many advanced applications (cartoon animation)

Drawing Vector > hard

Goal > convert freehand to vector: fidelity, simplicity, interactivity

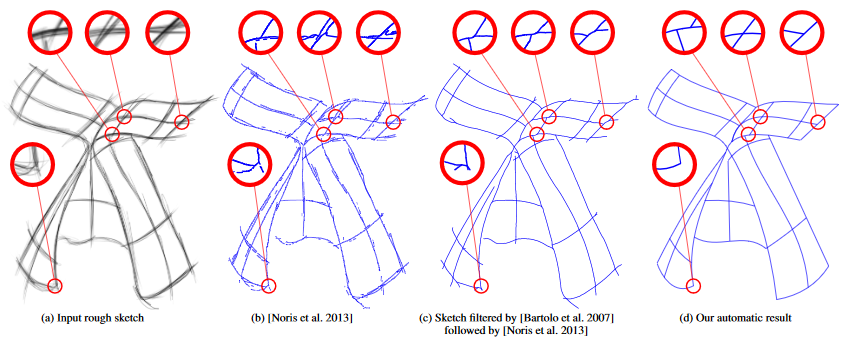
Existing vectorization > data fidelity, no simplicity > noticeable at line junctions

Algorithm balances fidelity with simplicity favouring the simplest interpretations overall

Data fidelity > goodness of fit of Bezier curve segments

Simplicity > the number and degree of curve segments that compose the drawing

2 Algorithm

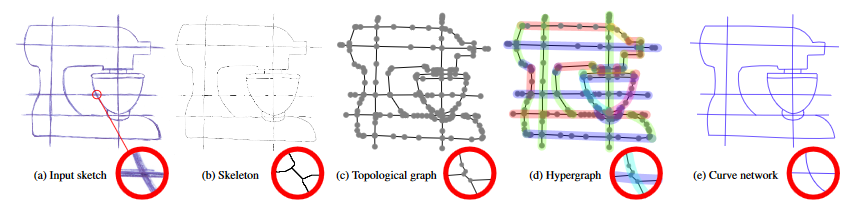
1 - extracting the skeleton

Region-based > skeleton as the frontiers between adjacent regions

morphological thinning > open curves

Output > network of 1-pixel width line

2 - vectorial representation > to identify which pixels should be grouped together to form curves

Grouping = topology of the drawing > represent it as a graph g = (V; E)

• nodes V correspond to the junctions and endpoints of the skeleton
• edges E correspond to the skeleton branches.

Edge E > Bezier curve segment

Improve accuracy > splitting the graph edges until the average fitting error of all Bezier curves is below 2 pixels.

Initial > over-segmented vectorization

3 - merge successive curve segments > reduce overall complexity - junctions.

model > rely on the concept of a hypergraph (is a generalization of a graph in which an edge can connect any number of vertices)

x = (V; Hx) be a hypergraph of the topological graph

goal: find x' < x (iteratively > transforming the graph)

compare > measure energy U

U is composed of two terms: fidelity,simplicity and parameter delta.

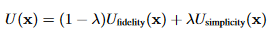
Fidelity term > the accuracy of a curve network as the sum of the fitting error of all its hyperedges

Simplicity term > by the number of hyperedges, favour curve networks whose Bezier curves have low degrees

Three types of operators

• Hyperedge merge and split (line)
• Bezier degree switch
• Hyperedge overlap and dissociation (junctions)

3 User interaction

Users can stop the optimization process at any time to specify constraints > three types:

Merge - Split - Freeze

Also, parameter T offers users useful control on the explorative behaviour of the optimization

4 Results and experiments

"Image Trace" (Adobe) > produce multiple curves, lines and short spurious curves at junctions on the filtered sketches

In contrast > almost identical results and recovers junctions with precision

Robustness > thick lines - the average error low

Performances > a few seconds to a few minutes

Limitations > only consider Bezier curves, no other primitives such as circular arcs. Delta parameter is global

Conclusion

clean, compact and easily editable artworks > to minimize the number of curves > disambiguating line junctions

Energy formulation will inspire novel algorithms dedicated to the simplification of digital drawings composed of vector strokes

Our idea of minimizing the complexity of the output representation also has great potential for the vectorization of colour images

---

A Bezier curve is a parametric curve used in computer graphics and related fields.

A quadratic Bezier curve

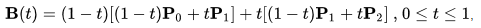
This paper describes one method to convert a sketch to a vector image.

Vector images have many features, for example, their lines are clean because a vector image is the combination of many math formulas and not, like a jpeg image, a set of pixels.