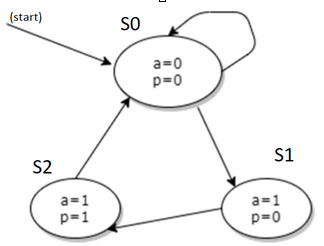
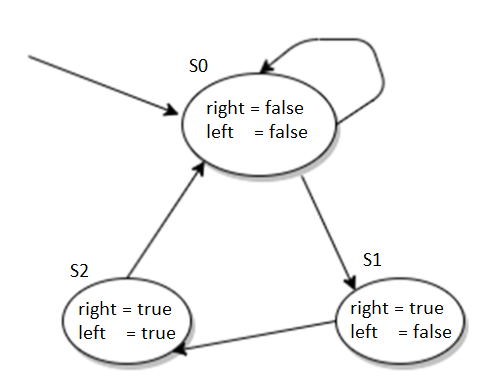
Dato il segunte modello scrivi il programma in NuSMV
Il codice in NuSMV
In NuSMV i file di input sono nella seguente forma:
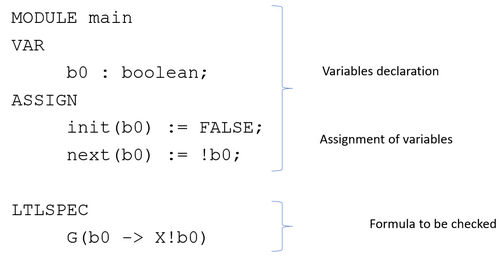
- specificate le variabili
- (eventualemente) inizializare le variabili
- descrivere come le variabili cambiano il loro stato
- formule che vogliamo controllare
Nel nostro modello abbiamo 2 variabili a e p. [VAR].
Le variabile sono inizializzate a false. Questo viene specificato nella parte ASSIGN.
Per descrivere come le variabili cambiano il loro stato abbiamo che
a in S0 è FALSE poi diventa TRUE in S1 ed S2
p in S0 e S1 è FALSE poi diventa TRUE in S2
Se volessimo scrivere la funzione NextStateA in pseudo-codice
bool NextStateA(s,a,p){
if (s == S0 && a == false && p == false)
return false; // da S0 ritorno a S0
if (s == S0 && a == false && p == true)
return true; // da S0 vado a S1
if (s == S1 && a == true && p == false)
return true; // da S1 ritorno a S2
if (s == S2 && a == true && p == false)
return true; // da S2 ritorno a S0
throw exception();
}
Per dare un significato più intuitivo a queste variabili e al problema sono state rinominate le variabili:
Il problema possiamo vederlo come un "modulo" nel
problema dei filosofi a cena.
Un filosofo può mangiare solamente se ha entrambe 2 bacchette.
Per poter iniziare a mangiare deve prendere la bacchetta alla sua destra.
Solamente una volta che ha la bacchetta nella mano destra può prendere quella alla
sua sinistra. Quando ha entrambe le bacchette può mangiare.
Una volta mangiato rilascia le bacchette.
La funzione NextRight diventa:

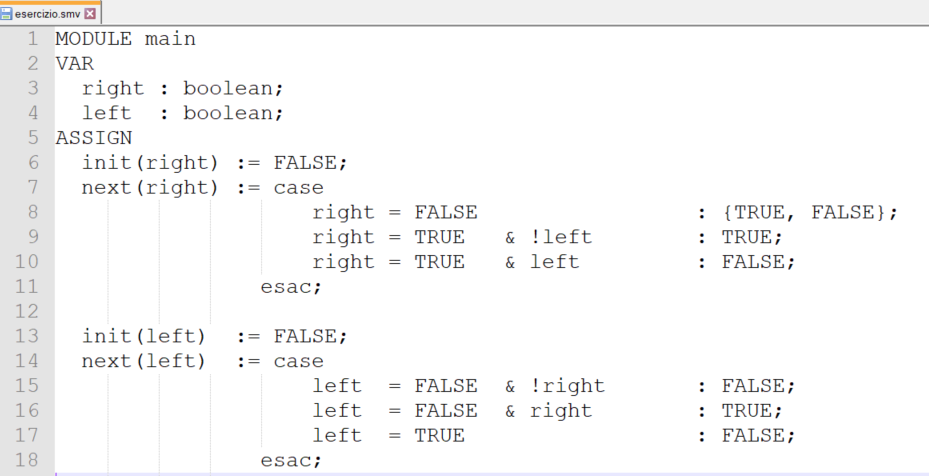
- La funziona NextRight ci dice che se la mano destra è libera [right = FALSE] posso sia non prendere la forchetta che prenderla {TRUE, FALSE}
- Se ho la forchetta con la mano destra ma la sinistra ancora non ha preso la forchetta allora non posso rilasciarla | right = TRUE & !left : TRUE; |
- Se invece ho preso la forchetta con la mano sinistra allora devo rilasciare la forchetta. | right = TRUE & left : FALSE; |
Inserendo anche le specifiche per la mano sinistra abbiamo il programma completo:
NuSMV - Esecuzione
Una volta scritto il programma si può eseguire NuSMV. NuSMV è una console, per eseguirlo si comando: NuSMV -int
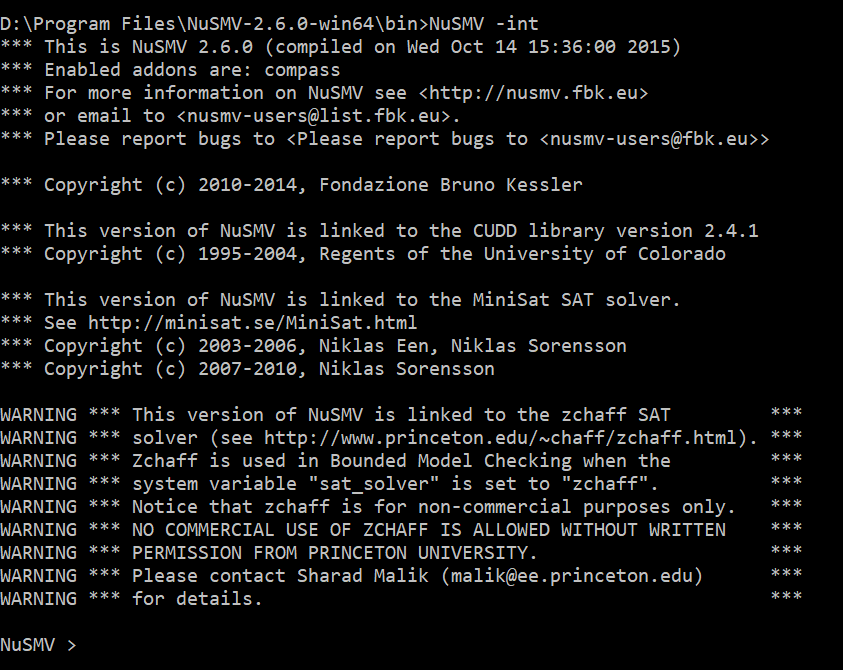
Successivamente si usano i comandi:
NuSMV > read_model -i esercizio.smv [per caricare il file il nostro modello]
NuSMV > go [per caricare il programma]
NuSMV > pick_state -i [per poter scegliere lo stato iniziale]
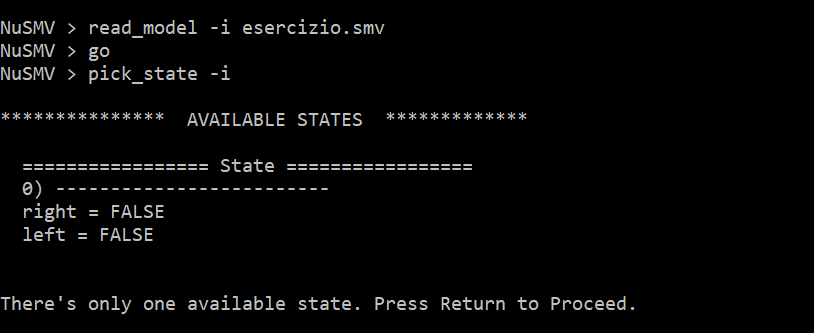
Nel nostro caso lo stato iniziale è S0 dato che right e left sono inizializate a false:
Per poter eseguire la simulazione usiamo il comando simulate -v -i 5. I parametri
- -v permette di stampare a video le variabili
- -i ci permette di scegliere il percorso
- -5 sono il numero di passi che vogliamo fare esporando il grafo
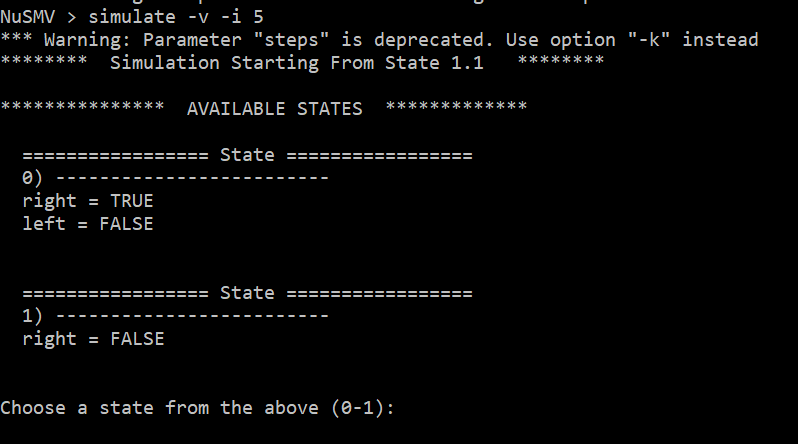
La prima (ed unica) scelta che possiamo fare è:
- prendere la forchetta e quindi spostarci nello stato S1 andando a modificare la variabile right che passa da false a true
- scegliere di restare nello stato S0 scegliendo di assegnare alla variabile right false
Se scegliamo di muoverci nello stato 1, siamo nuovamente in S0
Se invece scegliamo di prendere la forchetta di destra possiamo spostarci nello stato S1
Nello stato S1 non è possibile effetturare delle sceltre
in quanto c'è solamente uno stato disponibile.
Possiamo solamente spostarci nello stato S2.
Nello stato S2 non ci sono scelte possibili e quindi si può solamente ritornare in S0.
Esauriti i passi nella simulazione NuSMV stampa a video gli stati attraversati e il valori delle variabili durante il cammino.
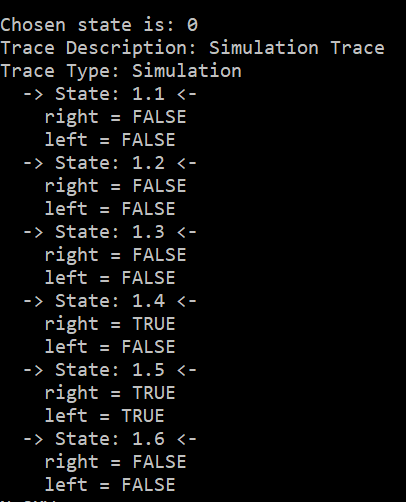
Siamo riusciti ad effetture una simulazione completa nel grafo,
controllando quindi che il programma è stato scritto correttamente
NuSMV - formule CTL
La prima operazione nell'analizzare le formule CTL è
creare un grafo con tutti i percorsi che è possibile percorrere partendo da S0.
Una volta creato un grafo con tutti i percorsi si possono analizzare le formule della consegna e controllare
in che stato sono vere.
1 - EX(right -> left)
In questa formula:
- E -> esiste un cammino (almeno un path sia vero)
- X -> next quindi nel passo successivo
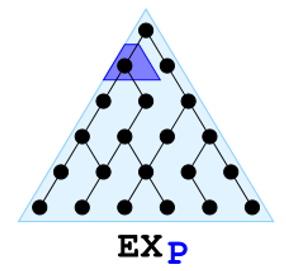
Intuizione
Dobbiamo controllare se esiste un un percorso in cui nello stato successivo
(right -> left) è vera. Gli stati successivi ad S0 sono S1 ed ancora S0

Visto che la formula chiedeva se esisteva almeno uno stato successivo in cui la formula
è vera riusciamo, anche grazie a NuSMV dimostrare,
che EX(right -> left) soddisfa il modello in S0.

Algoritmo di labeling
[teoria]
Per scroprire in quali stati la formula 𝜑 è vera usando il connettore
EX, possiamo usare la seguente definizione:
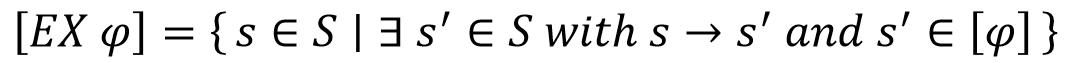
L'insieme degli stati che soddisfano la formula EX 𝜑 è vera se:
- s, che è un elemento appartentete all'insieme di tutti gli stati del modelo stati S (𝑠 ∈ 𝑆)
- esiste uno stato s' che appartiene all'insieme S (𝑠′ ∈ 𝑆)
- s' è in relazione con s (𝑤𝑖𝑡ℎ 𝑠 → 𝑠′)
- s' soddisfa la formula 𝜑 (𝑠′ ∈ 𝜑)
Ovvero se lo stato successivo rispetto a dove mi trovo soddisfa la forula 𝜑, EX(𝜑) è vera.

[svolgimento]

2 - EG(right -> EG(left))
In questa formula abbiamo 2 volte EG.
- E -> esiste un cammino
- G -> globally

Intuizione
Dobbiamo controllare se esiste un un percorso in cui (right -> EG(left)) è vera. Iniziamo il controllo elencando alcuni dei possibili percorsi:
- S0, S1, S2, S0, S1 ....
- S0, S0, S1, S2, S0, S1 ....
- S0, S0, S0, ...., S0 , ....
Path 1
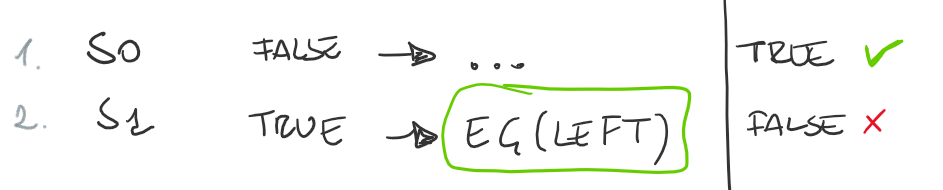
Al passo 1 possiamo calcolare direttamenete il risultato infatti se l'altecedente è falso la formula è vera.
Per calcolare al passo 2 se la formula è vera dobbiamo calcolare EG(Left). Dobbiamo vedere se nel futuro left è sempre vera. Questo non è il caso infatti nello stato S2 e nello stato S0 left è falsa
Come ulteriore esempio se eseguiamo solamente right-> EG(Left) modificando le variabili e partendo dallo stato S1
Abbiamo quindi compreso che nello stato S1 la formula è falsa.
Path 2
Nel secondo path, come nel precendete si incontra lo stato S1 quindi la formula è falsa.
Path 3
Nel terzo path il nostro stato è sempre lo stato S0.
Come abbiamo visto nel path1 nello stato S0 la formula è
vera. Abbiamo trovato un path per cui la formula EG(right -> EG(left)) è sempre vera.
Grazie a NuSMV riusciamo a dimostrare, che EG(right -> EG(left)) soddisfa il modello.

[Partendo dallo stato S1 al posto dello stato S0 la formula è falsa.]

Algoritmo di labeling
[teoria]

Per dimostrare se la formula EG è vera usiamo una equivalenza:
𝐸𝐺𝜑 ≡ 𝜑 ∧ 𝐸𝑋(𝐸𝐺𝜑)
Questo ci permette di usare riscrivere la formula e usare il connettivo 𝐸𝑋.
Successivamente si può usare la definizione 𝑃𝑟𝑒[𝜑] = 𝐸𝑋[𝜑] per poter
riscrivere la formula come:
[𝐸𝐺(𝜑)] = [𝜑] ∩ 𝑃𝑟𝑒([𝐸𝐺𝜑])
- [𝜑] gli stati dove la formula [𝜑] è vera INTERSEZIONE ∩
- la pre-immagine di [𝐸𝐺𝜑] <- (loop)
Si ricorsivamente calcolare X:= [EG𝜑] nel seguente modo:
passo 1 X1 := [𝜑] ---> tutti gli stati dove la formula 𝜑 è vera.
passo 2 X2 := X1 ∩ INTERSEZIONE PreImage(X1) ---> calcolo tutti gli stati che mi riescono a portare negli stati contenuti nelll'insieme X1
passo 3 Xc := X2 ∩ INTERSEZIONE PreImage(X2) ---> calcolo tutti gli stati che mi riescono a portare negli stati contenuti nelll'insieme X2
passo n Xn := Xn+1 ∩ INTERSEZIONE PreImage(Xn+1) ---> calcolo tutti gli stati che mi riescono a portare negli stati contenuti nelll'insieme Xn+1
Quando il passo successivo è uguale al passo precendente --> si è raggiunto un "punto fisso" e quindi è possibile fermarsi
[svolgimento]
La prima operazione da svolgere è riscrivere la formula usando l'equivalenza che utilizza la funzione pre-image

Ricorsivamente si possono calcolare i passi successivi

Bisogna successivamente calcolare la pre-image

Si devono trovare gli stati in cui [EG(p)] è vero

Si può riscrivere l'implicazione con dei connettivi booleani

L'intersezione ci permette di trovare lo stato in cui la formula è vera: {S0}

3 - EF(right) -> EG(left)
In questa formula:
- E -> esiste un cammino
- F -> finally, nel futuro
- G -> globally, sempre nel futuro
Intuizione
La formula 𝜑 è la composizione di 2 formule EF(right) ed EG(left)
EF(right) controlla che nel futuro right diventi vera almeno una volta.
EG(left) controlla che nel futuro left sia sempre vera. Questo è sempre falso.

- se percorriamo sempre il grafo S0, S0, S0, S0, S0, ... abbiamo che la prima parte dell'implicazione EF(right) è sempre falsa e quindi che la formula 𝜑 è sempre vera
- se percorriamo il percorso S0,S1,S2,S0, ... EF(right) diventa vera ma poichè EG(left) è sempre falsa, la formula 𝜑 è sempre falsa
Quando eseguiamo l'esercizio il programma restituisce che la formula è falsa.

Algoritmo di labeling
[teoria]
Possiamo riscrivere EF(𝜑) come E(true UNTILL 𝜑)

Visto che true è ovviamente sempre vero si riesce ad esprimere che la formula 𝜑 sarà vera nel futuro

Per calcolare tutti i passaggi usiamo la seguente equivalenza:

𝐸(𝜑 𝑈 𝜓 ) ≡ 𝜓 ∨ ( 𝜑 ∧ 𝐸𝑋(𝐸 𝜑𝑈𝜓 )) ----> phi untill psi
Questa uguaglianza si può riassumere come:
𝜓 deve essere vera nello stato in cui stiamo partendo OR
𝜑 deve essere vera nello stato in cui stiamo partendo AND nello stato successivo dobbiamo controllare ancora che 𝐸 ( 𝜑 𝑈 𝜓) <-- loop
Possiamo definirre [𝐸 ( 𝜑 𝑈 𝜓)] come
[𝜓] ∪ ( [𝜑] ∩ PRE-IMAGES( [(𝐸(𝜑𝑈𝜓))
- stati in cui 𝜓 è vera UNIONE
- stati in cui 𝜑 è vera INTERSEZIONE
- PRE-IMAGES [𝐸(𝜑𝑈𝜓)]
Si riesce a calcolare X:= [𝐸 ( 𝜑 𝑈 𝜓)] con l'induzione
- X1 := [𝜓] ---> iniziamo calcolando gli stati in cui 𝜓 è vera, AGGIUNGIAMO
- 𝑋2 ∶= 𝑋1 ∪ ( [𝜑] ∩ 𝑃𝑟𝑒 (𝑋1) ) X1 AGGIUNGIAMO stati in cui ( 𝜑 è vera INTERSEZIONE pre-images X1 )
- 𝑋3 ∶= 𝑋2 ∪ ( [𝜑] ∩ 𝑃𝑟𝑒 (𝑋2))
- 𝑋n+1 ∶= 𝑋n ∪ ( [𝜑] ∩ 𝑃𝑟𝑒 (𝑋n))
Quando Xn+1 è uguale a Xn allora si è raggiunto un punto di uscita nell'algoritmo.
[svolgimento]
La prima espressione da calcolare è EF(right).
Può essere scritta anche in quest'altro modo:

Ricorsivamente si possono calcolare i passi successivi.
Nel primo passo {S1,S2} soddisfa la formula RIGHT e si "salvano" in X1

Nel passo successivo si calcolano i passi precendenti a {S1,S2}. L'insieme finale è {S0,S1,S2}

Si può riscrivere l'implicazione e quindi calcolare gli stati dove la formula è vera

Non ci sono stati, e quindi la formula è sempre falsa
4 - EF(right AND left)
In questa formula:
- E -> esiste un cammino
- F -> finally, nel futuro
Intuizione
La formula 𝜑 vuole scoprire se nel futuro è possibile che ci sia uno stato in cui right e left sono veri
Quando eseguiamo l'esercizio il programma restituisce che la formula è vera.

Algoritmo di labeling
[teoria]
Come nell'esempio di prima 111
[svolgimento]
Il primo passo è da calcolare è EF(right AND left).
Può essere scritta anche in quest'altro modo:
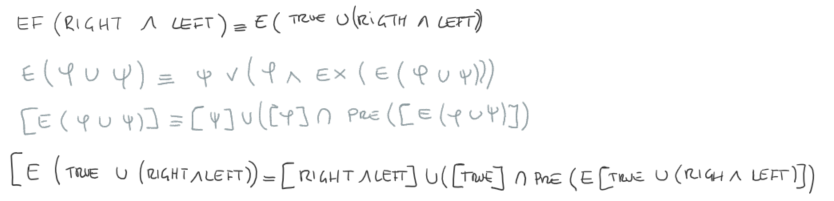
Ricorsivamente si possono calcolare i passi successivi.
Nel primo passo solo S2 soddisfa la formula

Nel secondo passo si trova il passo precedente che porta ad S2 ovvero S1.
L'insieme delle soluzioni è {S2,S1}
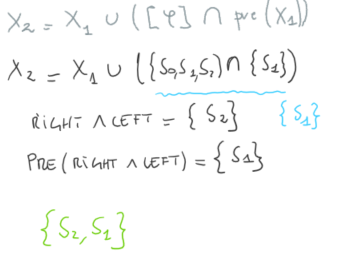
Il passo successivo è aggiungere gli stati che possono portare a {S2,21}
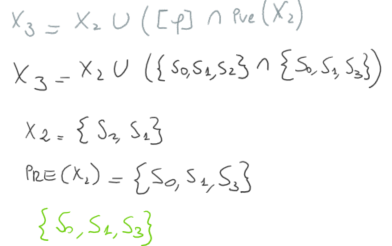
{S0,S1,S2} soddisfano la forumula, che quindi in ogni stato è vera
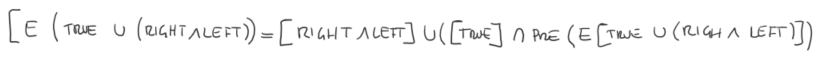
Symbolic Model Checking
A partire da un modello di transizione 𝑀 = (𝑆, →, 𝐿) possiamo codificare ogni stato in base ai valori delle variabili che lo compongono. Nel nostro esercizio il primo valore rappresenta la variabile right la seconda la variabile left. Avendo solo 2 variabili sono sufficienti 2 cifre.

Quindi 01 vuol dire che right è falso mentre left è vero.
Una volta fissato l'ordine delle variabili si può rappresentare il modello anche in un quest'altro modo.

Con questa codifica ogni stato può essere rappresentato da una formula:

Viene indicata con e(s) la formula associata ad uno stato. Ogni insieme di stati Q ⊆ 𝑆 può quindi essere associato alla formula.

Nel nostro esercizio abbiamo:

Per rappresentare le transizioni del modello si inizia creado n uteriori variabili. Le nuove variabili saranno tante quante sono le variabili nel nel sistema.
La prima operazione è la costruzione di una tabella. Ogni arco nel sistema è rappresentato da una riga in tabella.
Leggendo la riga la prima metà delle colonne codifica lo stato dove sono, la seconda metà delle colonne codifica lo stato successivo.
Nel nostro esercizio avvremmo la seguente tabella:

Una volta creata la tabella possiamo scrivere la formula in DNS.
Prendiamo il valore negato se la variabile è false mentre invece prendiamo il valore non negato se la variabile è positiva.
La formula risultate sarà vera se almeno una "riga" sarà vera. Nel nostro esempio la formula sarà:

Un altro metodo per scrivere la formula è partire direttamente dal programma scritto in NuSMV.
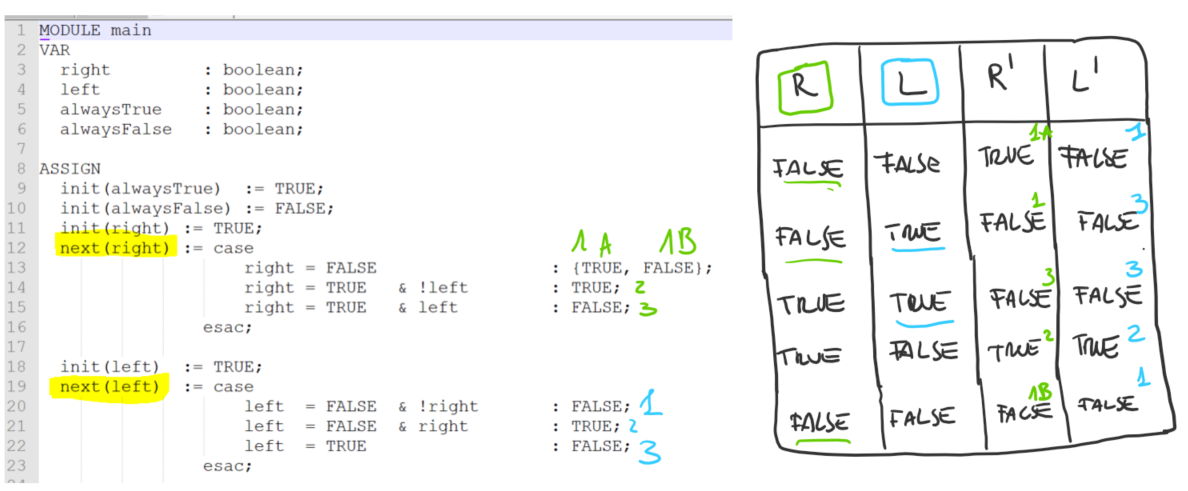
Una volta ottenuta la formula possiamo analizzare il grafo OBDD associato:


Il grafo è costruito collegando le varie variabili tra di loro. L'ordine delle variabili è fondamentale per crere il grafo infatti cambiando l'ordine cambia anche il grafo.
L'ordine che è stato seguito in questo caso è stato X1, X2, X1', X2'
Formula
https://www.erpelstolz.at/gateway/formular-uk-zentral.html
(¬A ∧ ¬B ∧ ¬C ∧ ¬D)∨
(¬A ∧ ¬B ∧ C ∧ ¬D)∨
(A ∧ ¬B ∧ C ∧ D)∨
(A ∧ B ∧ ¬C ∧ ¬D)
Files
Risorse Utili:
Tutotial -> http://nusmv.fbk.eu/NuSMV/userman/v11/html/nusmv_2.html#SEC2
Model Checking playlist -> https://www.youtube.com/channel/UCUXDMaaobCO1He1HBiFZnPQ/videos
Slide in italiano -> https://person.dibris.unige.it/delzanno-giorgio/MCG/note.pdf
Manuale utente -> http://nusmv.fbk.eu/NuSMV/userman/v26/nusmv.pdf